The Ultimate Trisection

The 22 May 2025 Trisection’s microscopic intersection cluster can present difficulties due to its small size. Working at the extreme limits of the software, elements get displaced while zooming in and at high magnification, operations such as placing points, lines or circles can become misaligned, misplaced or dropped entirely. Importantly, variations of the last few decimal places can also inexplicably occur. A clear example of this is when the same angle measured in both clockwise and counter-clockwise directions produces two different results. 

I explored other software programs and found GeoGebra to be the best, but problems persisted on several platforms and three different operating systems. So to avoid the anomalies, I searched for a way to model elements of the construction at a larger scale.

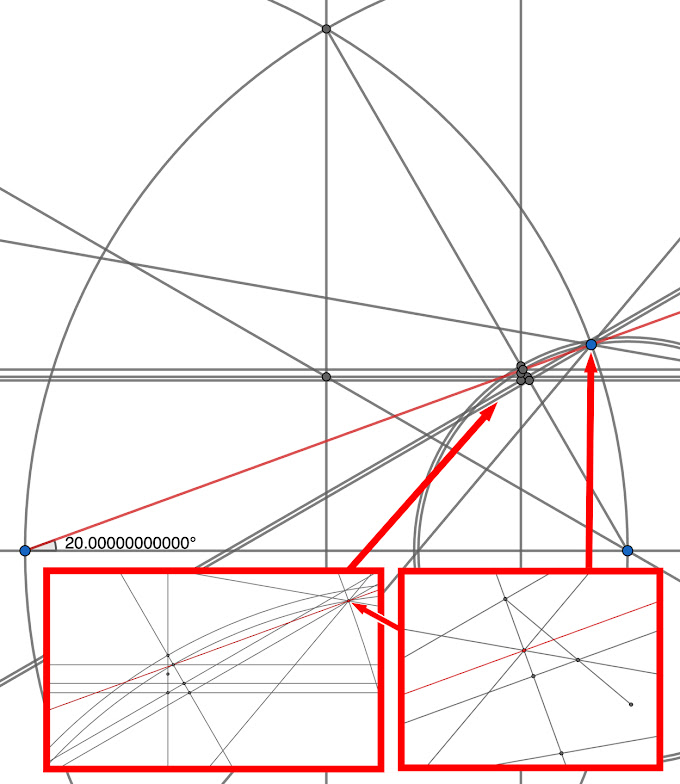
Starting with a 60° angle, I constructed a larger representation of the microscopic intersection. Instead of plotting thirds of the primary chord’s segment between the perpendicular and its associated arc, the arc beneath is placed at midpoint and the parallel of the perpendicular is placed below at a quarter. 

The perpendicular and its arc intersect the primary arc similarly to the microscopic construct, except approximately 800 times larger. The 30° angle and bisector can be placed in the same fashion, and the angle arm bisector and angle bisector intersect inside the arc, same as the microscopic analog. The correct angle, however, doesn't appear at this intersection, though constructions at this juncture seems more manageable due to increased size. But at the last stage, things get much smaller.

An equilateral-like structure made up of the perpendicular bisector, angle bisector and a segment of the primary arc is formed at the interior of the primary arc. Perpendicular bisectors placed between apexes on each of its segments converge centrally without intersecting opposite apexes. And the perpendicular bisector intersecting the arc segment misses a 20° reference point (B’) on the primary arc by 0.000000022319352 (primary angle base length of 12). However, placing a line parallel to the arc’s bisector at the opposite vertex forms a microscopic triangle with a height of 0.000000044638661 adjacent to the structure's center.

The microscopic triangle is used to plot the primary angle's trisecting Point Z between the parallels. A line from Point Z intersecting the primary angle’s apex also intersects reference Point B' at the primary’s arc, accurately trisecting the 60° angle to fifteen decimal places. 

 

This demonstrates an additional solution to 60° Euclidean angle trisection and functions on arbitrary acute angles as well. However, it still requires microscopic operations at the cusp of the software's capabilities. 

  

80° Trisection demonstrating directional disparity in Reference Angle (blue) & Constructed Angle (red).

Until greater hardware-software precision is achieved, my Euclidean trisection solutions can only deeply challenge the accepted impossibility theories without unequivocal certainty. So I'll be leaving off at this point until greater computational power can be leveraged. 

Thank you.

POSTSCRIPT 22 December 2025: When the original trisection is constructed using a primary circle with a radius of 180/π, linear calibrations equal angular degrees and provide arc length measurement. In this construction, the microscopic length of the angle's chord is equal to its arc, which measures 0.000377784319883°. This is theoretically impossible, though as it is around 1/952,924.674—close to a millionth—of the circle's circumference, the section is nearly a line. However, this exposes a computational limit. 

The angle and the chord of the microscopic angle arc are equal at computational limits.

Due to the sketchiness of these results, a shadow seems to fall on the 22 May solution. However, even if this trisection reaches into the ad infinitum realm, a solution still occurs when a circle with an infinite radius straightens into a line due to the employment of linear trisection. 

In the end, if there's anything to be learned here, it is that computers still need a great deal of work, warranting a deep dive into ternary computing. Ternary computers will be more efficient and capable of increased accuracy due to the greater numerical resolution of trits over bits. In addition, binary applications will still function using binary-coded ternary (BCT). Here's an introduction to ternary computing with some of its latest breakthroughs: