60° Trisection Goes Big!

Magnified Details of the 60° Trisection—

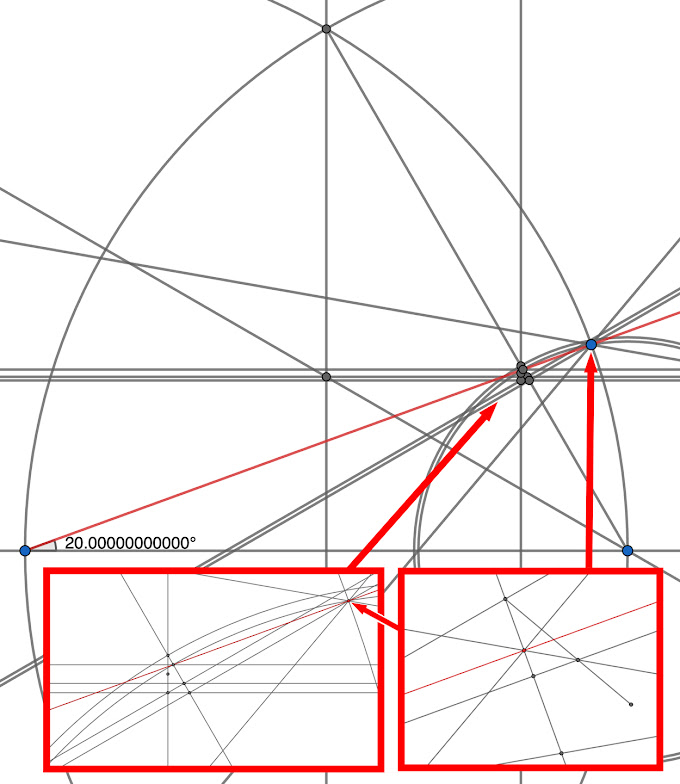
I found a way to trisect a 60° angle with Euclidean construction simulated on a computer using the GeoGebra Geometry Calculator. The software allows a user to zoom into details and manage minuscule structures, acceptable according to Euclidean principles. And GeoGebra's drawing board can be configured to display Cartesian coordinates, which are defined as centimeters in the following examples to provide a sense of scale.

The construction employs a sequence of three progressively smaller linear thirds to geometrically bridge the length disparity between one third of the primary angle's chord and one third of its arc. 

With the 60° primary angle having a base width and arc radius of 14 cm, the construction culminates with operations executed within a cluster of three intersections the size of a single bacterium, 2.66 µm x 0.923 µm. This grouping is so tiny that if it were constructed using the finest pen on a sheet of paper the size of a room, one would be hard-pressed to distinguish it from a single-point intersection—a 14-foot base segment would produce an intersection cluster of 0.003" x 0.001".

In the final step, a segment of less than a half micron is trisected to yield the constructed Point U, which measures 20.000000000000000°, one third of the primary angle. A verification reference Point B' placed at exactly 20° by the software is indistinguishable from Point U at a magnification of 3,000,000x. 

Although collinear, Point U and Point B' do not overlap. The magnification can be increased by the software to obtain a closeup view of the common angle arm. At a magnification of 280,000,000,000x, each point becomes distinct and both are in alignment on the same 20° angle arm with less than a picometer of separation—128 times smaller than a hydrogen atom. 

This illustrates the disparity in size required for this solution and may account for the presumed impossibility of angle trisection in the past.  The power of the computer demonstrates that 60° Euclidean angle trisection is achievable within measurable limits, making it far from impossible.

3,000,000x magnified view of the microscopic three-way intersection, which in a normal view appears as a single intersection smaller than a bacterium. 

 

This is the tiny linear trisection where constructed Point U is placed. At this magnification, reference Point B' eclipses Point U. 

 

At the maximum simulated magnification, constructed Point U and reference Point B' are closer than one picometer and both are aligned on the blue ray defining a 20° angle.

 

Overall view of construction showing Cartesian coordinates with grid. 

 

 ***

 

 Videos exploring the 75° Trisection:

 

GeoGebra’s drawing board may be configured to display Cartesian coordinates and objects are measured in those terms, which is useful, as the trisection employs a sequence of three progressively smaller linear thirds. A 75° primary angle with an arc radius of 12-inches was chosen for this video to provide a sense of scale. The coordinates are defined as inches, with inches converted to metric at the microscopic levels, reaching down to the atomic level. 

 

The construction culminates with operations executed within a cluster of three intersections the size of a bacterial cell, 21.6µm by 4.8µm, with points capturing an arc ~1/200,000th of the primary circle's circumference. In the final step, a segment of 2.4 microns is trisected to yield the constructed Point Z, which measures 25.000000000000000°, one third of the primary angle. A verification reference Point D' placed at exactly 25° by the software is indistinguishable from Point Z at a magnification of around 3,000,000x.  

 

Although collinear, Point Z and Point D' do not actually overlap. The magnification can be increased by the software to the range of 200,000,000,000x to obtain a closeup view of the common angle arm. At this magnification, each point becomes distinct and both are in alignment on the same 25° angle arm with less than 33.5 picometers of separation—around the size of a helium atom! Placed one mile from the primary apex, an additional reference point falls precisely on the constructed 25° angle arm. 

 

A short video illustrating 60° Trisection steps:

 

 

 

ISNI 0000 0000 3555 6165