The Impossible Trisection

60° TRISECTION MADE POSSIBLE. 

The chasm between 60° and 20° angles was thought to be so wide that after two millennia of failing to bridge it, euclidean angle trisection was finally written off by mathematical theory back in the 1830s. The claim was that trisection had been solved by proving it was mathematically impossible. But many trisection diehards soldiered on, and those who assailed mathematicians with drawings were routinely dismissed out-of-hand. Despite its deep influence on mathematics, no one would take the question of trisection seriously again. 

I became one of those diehards. I couldn't agree that even the most rigorous mathematics could account for all the variables or prove impossibility. So I toiled on the problem and thought I'd nailed it a few years ago, but was off by a few hundredths of a degree after testing with better software. Through the process, I'd grown to appreciate geometry and persisted, this time using GeoGebra's Geometry Calculator. Not really expecting to find a solution, I did so for the enjoyment of learning. Besides, getting it wrong was always the right answer, because after all, it was impossible.

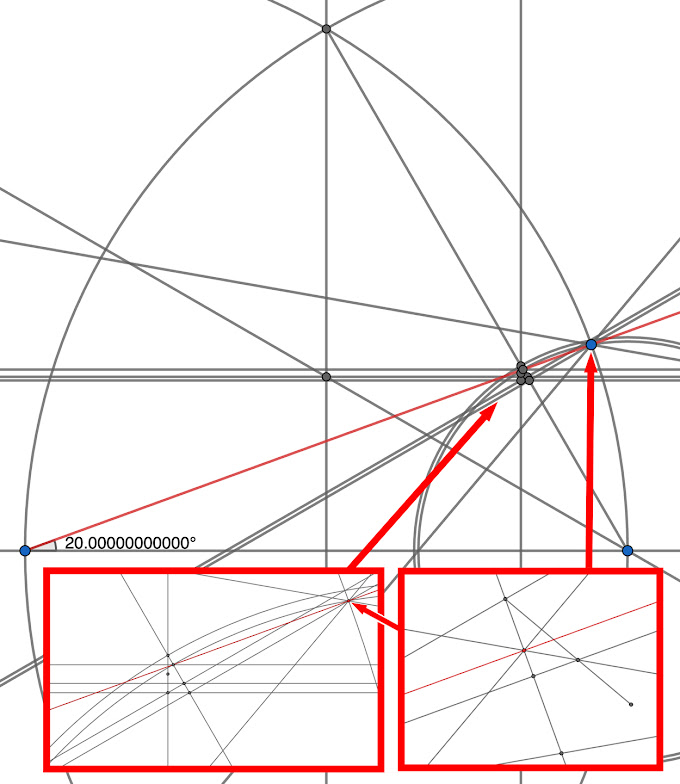
The other day, though, I got to pondering the difference between a third of a 60° angle's chord, which was accepted as constructible, and that of its arc, which wasn't. The objective of bridging the difference became a matter of blazing a path using tools of perpendiculars, parallels, bisectors, arcs, and mainly, linear thirds. Starting with a third of the angle's chord naturally led to the perpendicular and its intersection with the arc. Then arcing back to the difference led to placement of thirds in tandem, ending up at a microscopic triangular structure of two arcs and a line segment the size of a bacterium, visible only by computer. A point was placed at a linear third within the microscopic structure. Measuring it back to the vertex of the 60° angle, I couldn't believe it—a clean 20°—it worked! I had trisected the 60° angle.

If the mathematical impossibility theory lingers, consider that this trisection employs computer-assisted construction able to display microscopic structures invisible to the naked eye, unnoticed through millennia and unanticipated in the 1830s. And the use of linear thirds in operations surrounding the proportion of a chord segment to its arc was not addressed by the impossibility theory. By the application of digital computation using precision Cartesian coordinates, the construction clearly produces a 20° angle to fifteen decimal places. So with quadrillion-to-one certainty, euclidean trisection of a 60° angle has been achieved. 

As it turns out, the chasm between 60° and 20° wasn't impossibly wide at all, but so minuscule it was just impossible to see—until now.

The trisection may appear messy on the macro scale, but is beautiful in the microscopic view of its endpoint (right).
 


Verification: The constructed trisecting angle (Point U) compared to GeoGebra's "Angle with Given Size" (reference Point G'). Both points fall on the same angle arm in a magnified view & both measure exactly the same. 
   

I've made videos demonstrating the trisection steps-by-step and encourage you to try it in GeoGebra or other software. You might find geometry enjoyable, too. And by the way, squaring the circle is still up for grabs.  


 ISNI 0000 0000 3555 6165

Comments

Post a Comment

Popular posts from this blog

60° Trisection Goes Big!

Image
Magnified Details of the 60° Trisection— I found a way to trisect a 60° angle with Euclidean construction simulated on a computer using the GeoGebra Geometry Calculator . The software allows a user to zoom into details and manage minuscule structures, acceptable according to Euclidean principles. And GeoGebra's drawing board can be configured to display Cartesian coordinates, which are defined as centimeters in the following examples to provide a sense of scale. The construction employs a sequence of three progressively smaller linear thirds to geometrically bridge the length disparity between one third of the primary angle's chord and one third of its arc.  With the 60° primary angle having a base width and arc radius of 14 cm, the construction culminates with operations executed within a cluster of three intersections the size of a single bacterium, 2.66 µm x 0.923 µm. This grouping is so tiny that if it were constructed using the finest pen on a sheet of pape...
Read more

The Ultimate Trisection

Image
The 22 May 2025 Trisection’s microscopic intersection cluster can present difficulties due to its small size. Working at the extreme limits of the software, elements get displaced while zooming in and at high magnification, operations such as placing points, lines or circles can become misaligned, misplaced or dropped entirely. Importantly, variations of the last few decimal places can also inexplicably occur. A clear example of this is when the same angle measured in both clockwise and counter-clockwise directions produces two different results.  I explored other software programs and found GeoGebra to be the best, but problems persisted on several platforms and three different operating systems. So to avoid the anomalies, I searched for a way to model elements of the construction at a larger scale. Starting with a 60° angle, I constructed a larger representation of the microscopic intersection. Instead of plotting thirds of the primary chord’s segment between the perpendicular an...
Read more