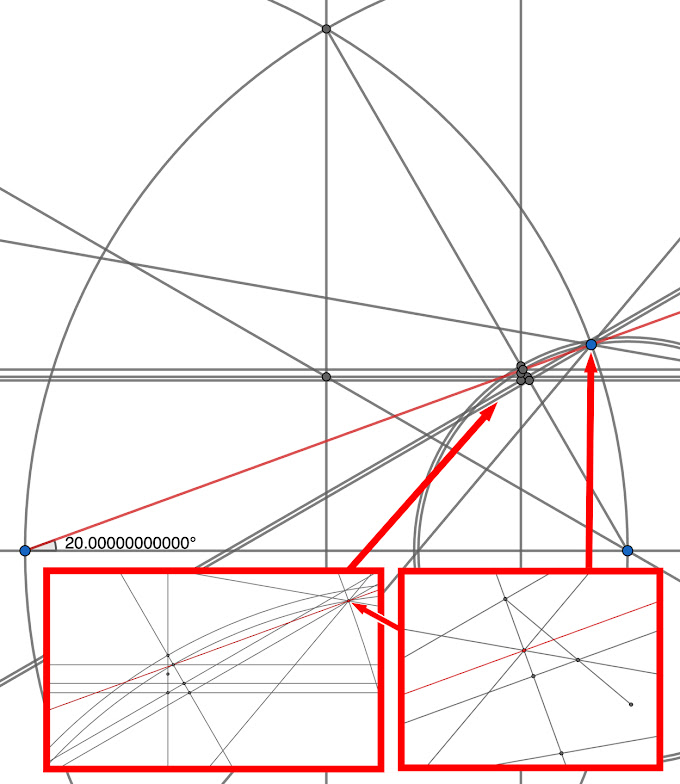
Approaching a proof, I'd been working on modeling constructs capturing larger segments of the primary angle arc and came up with a more simplified trisection method. This produced an astounding reference-construction deviation of only 0.000000000000001 and was worthy of what I thought would be my final video, the "Ultimate Trisection" of February 15, 2026. With a 12-inch base, it produced a deviation equivalent to one thirty-third the diameter of a hydrogen atom's nucleus—it couldn't get better than that! But it could and it did. I didn't throw in the towel and on March 18, 2026, hit on new final steps leading to zero deviation between my constructed angle and the computer derived reference point. This was a little embarrassing, as I'd already put the matter to bed. I started to make another video, flip-flopped, put it off until yesterday.                                     ...

The 22 May 2025 Trisection’s microscopic intersection cluster can present difficulties due to its small size. Working at the extreme limits of the software, elements get displaced while zooming in and at high magnification, operations such as placing points, lines or circles can become misaligned, misplaced or dropped entirely. Importantly, variations of the last few decimal places can also inexplicably occur. A clear example of this is when the same angle measured in both clockwise and counter-clockwise directions produces two different results.  I explored other software programs and found GeoGebra to be the best, but problems persisted on several platforms and three different operating systems. So to avoid the anomalies, I searched for a way to model elements of the construction at a larger scale. Starting with a 60° angle, I constructed a larger representation of the microscopic intersection. Instead of plotting thirds of the primary chord’s segment between the perpendicular an...

Magnified Details of the 60° Trisection— I found a way to trisect a 60° angle with Euclidean construction simulated on a computer using the GeoGebra Geometry Calculator . The software allows a user to zoom into details and manage minuscule structures, acceptable according to Euclidean principles. And GeoGebra's drawing board can be configured to display Cartesian coordinates, which are defined as centimeters in the following examples to provide a sense of scale. The construction employs a sequence of three progressively smaller linear thirds to geometrically bridge the length disparity between one third of the primary angle's chord and one third of its arc.  With the 60° primary angle having a base width and arc radius of 14 cm, the construction culminates with operations executed within a cluster of three intersections the size of a single bacterium, 2.66 µm x 0.923 µm. This grouping is so tiny that if it were constructed using the finest pen on a sheet of pape...

60° TRISECTION MADE POSSIBLE.  The chasm between 60° and 20° angles was thought to be so wide that after two millennia of failing to bridge it, euclidean angle trisection was finally written off by mathematical theory back in the 1830s. The claim was that trisection had been solved by proving it was mathematically impossible. But many trisection diehards soldiered on, and those who assailed mathematicians with drawings were routinely dismissed out-of-hand. Despite its deep influence on mathematics, no one would take the question of trisection seriously again.  I became one of those diehards. I couldn't agree that even the most rigorous mathematics could account for all the variables or prove impossibility. So I toiled on the problem and thought I'd nailed it a few years ago, but was off by a few hundredths of a degree after testing with better software. Through the process, I'd grown to appreciate geometry and persisted, this time using GeoGebra's Geometry Calculator. N...

 A handful of birds in the bush around Oregon:   Sooty Fox Sparrow, 1/320sec f/9 ISO400, Olympus 100-400 at 400mm Spotted Towhee, 1/320sec f/8 ISO200, Olympus 75-300 at 300mm American Robin, 1/50sec f/8 ISO 400, Olympus 100-400 at 400mm White Crowned Sparrow, 1/320sec f/8 ISO400, Olympus 100-400 at 400mm   Red-winged Blackbird, 1/320sec f/8, ISO 400, Olympus 100-400 at 400mm A ruffled European Starling, 1/250sec f/6.3, ISO 500, Olympus 100-400 at 400mm Great Blue Heron, 1/1000sec f/2.8 ISO200, Olympus 45mm f/1.8  Olympus OM-D EM-1 Mark II with the Olympus M.Zuiko ED 100-400mm f/5-6.3 IS lens. A grip attached to the lens tripod collar helps steady the camera and improves handling. An OpTech wrist strap is mounted clear of the controls on a camera-specific Arca-type base.   All images are original works by the author ©2023

观音因在那里种花而被逐出地狱。 Guan Yin was kicked out of hell for planting flowers there. I usually take my camera to Al's Garden & Home in Woodburn, Oregon, and visit the flowers while we shop. Flowers hold a special fascination for me, with their mysterious variations of color, form, scent—flowers epitomize the Life Force and are its treasure. Along with the Olympus M.Zuiko Digital ED 60mm f/2.8 Macro, my mainstay flower lens, I brought the Olympus M.Zuiko ED 12-100 f/4 IS PRO travel zoom to see how it would do. While the zoom feature of the 12-100 is nice to use and the lens has legendary image quality and a ~1:3 closeup ratio, it just wasn't a substitute for the macro. So after a few shots, the travel lens was put away.  Like an old friend, the 60mm f/2.8 Macro never lets me down. I had a copy back in the original E-M5 days, but eBayed it when I had to have the latest-and-greatest, very excellent Sony 90mm Macro to go onto the full-frame A7RII that had pushed its way into the camera...